人教版高中·高二数学选修2-2《数学归纳法》（第2.2.3课时）PPT精品课件

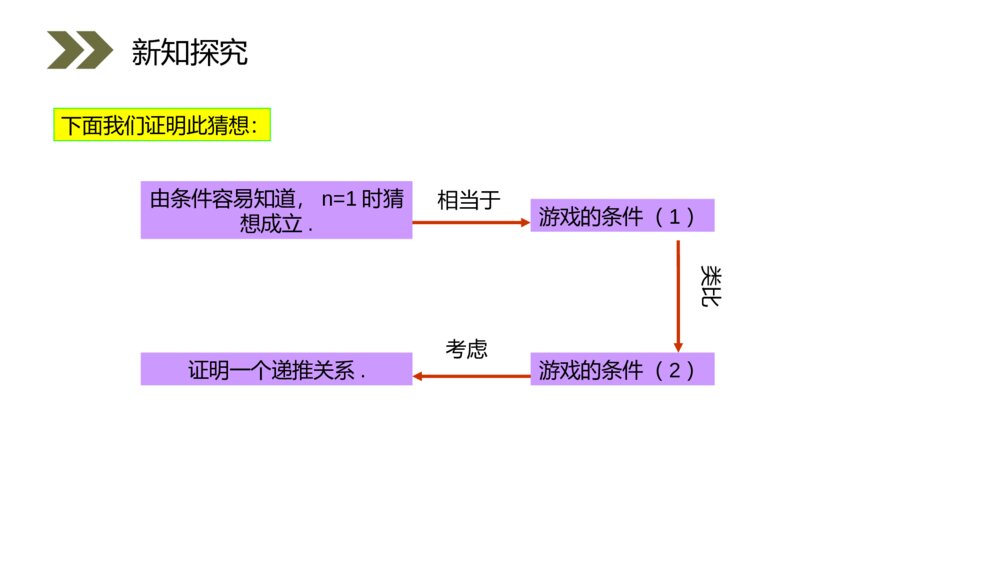
讲解人：XXX时间：2020.6.1PEOPLE\'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-22.3数学归纳法第2章推理与证明人教版高中数学选修2-2nnn+1naaa=(n=123)1+a1对于数列{}，已知a=1，，，，，此数列的通项公式是什么？n1a=.n通过对n=1，2，3，4前4项的归纳，我们已经猜出其通项公式为课前导入nnn+1naaa=(n=123)1+a1对于数列{}，已知a=1，，，，，此数列的通项公式是什么？n1a=.n这个猜想对前4项成立，但是，能肯定它对后续的项也成立吗？这个猜想需要证明，自然地，我们会想到从n=5开始一个个往下验证.这个方法可行吗?课前导入我们来分析此方法：一般来说，与正整数n有关的命题，当n比较小时可以逐个验证，但当n比较大时，验证起来会很麻烦.特别是证明n取所有正整数都成立的命题时，逐一验证是不可能的.因此，从n=5开始逐个往下验证的想法价值不大.我们需要另辟蹊径，寻求一种方法：通过有限个步骤的推理，证明n取所有正整数都成立.课前导入大家都听说过多米诺骨牌游戏，这是一种码放骨牌的游戏，码放时保证任意相邻的两块骨牌，若前一块骨牌倒下，则一定导致后一块骨牌也倒下.只要推到第一块骨牌，由于第一块骨牌倒下，就可导致第二块骨牌倒下；而第二块骨牌倒下，就可导致第三块骨牌倒下……最后，不论有多少块骨牌，都能全部倒下.新知探究这个游戏中，能使所有多米诺骨牌全部倒下的条件是什么？探究思考…动动脑想一想，自己总结出倒下的条件.新知探究只要满足以下两个条件，所有多米诺骨牌就都能倒下：（1）第一块骨牌倒下；（2）任意相邻的两块骨牌，前一块倒下一定导致后一块倒下；你认为条件（2）的作用是什么？新知探究可以看出，条件（2）事实上给出了一个递推关系：当第k块倒下时，相邻的第k+1块也倒下.这样，只要第一块骨牌倒下，其他所有的骨牌就能够相继倒下.事实上，无论有多少块骨牌，只要保证(1)(2)成立，那么所有的骨牌一定可以全部倒下.新知探究大家现在能证明这个猜想吗？这个猜想和多米诺骨牌游戏有相似性吗？你能类比多米诺骨牌游戏解决这个问题吗？n1nn+1nn{a}a=1aa=(n=123)1+a1a=.n对于数列，已知，，，，，此数列的通项公式新知探究n1nn+1nn{a}a=1aa=(n=123)1+a1a=.n对于数列，已知，，，，，此数列的通项公式游戏的条件（1）由条件容易知道，n=1时猜想成立.游戏的条件（2）下面我们证明此猜想：相当于类比证明一个递推关系.考虑新知探究继续解答……事实上，如果，那么，即时猜想也成立kkk+1ka1a=a=k1+a11k==n=k+1.1k+11+k如果n=k时猜想成立，即，那么当n=k+1时猜想也成立，即.k1a=kk+11a=k+1新知探究事实上，如果，那么，即时猜想也成立kkk+1ka1a=a=k1+a11k==n=k+1.1k+11+kk1a=kk+11a=k+1这样，对于猜想，由已知n=1成立，就有n=2也成立；n=2成立，就有n=3也成立；n=3成立，就有n=4也成立；n=4成立，就有n=5也成立······所以，对任意的正整数n，猜想都成立.继续解答……此猜想正确，即n1a=.n此数列的通项公式新知探究n1a=.n此数列的通项公式一般地，证明一个与正整数n有关的命题，可按下列步骤进行：1.证明当n取第一个值n0时命题成立；这种证明方法就叫做　　数学归纳法.归纳奠基归纳递推新知探究2.假设当n=k(kN*，k≥n0)时命题成立，证明当n=k+1时命题也成立.用框图来表示此证明方法:验证n=n0时命题成立.当n=k(k≥n0)时命题成立，证明n=k+1时命题也成立.归纳奠基归纳递推命题对从n0开始所有的正整数n都成立.新知探究用数学归纳法证题时,应注意的事项:“归纳奠基”和“归纳递推”两个步骤缺一不可，其中第一步是命题递推的基础，第二步是命题递推的根据.具体说明如下：(1)第一步——归纳奠基•必须有第一步，如果没有第一步，证明不可靠；新知探究•用数学归纳法进行证明时，第一步从n等于几开始，要根据具体问题而定.如果要证明的命题是对不小于的全体正整数都成立，则要从n=证起；0n0n如果要证明的命题是对全体正整数都成立的，则要从n=1证起；一般来说如果要证明的命题是对全体自然数(包括0)都成立的，则要从n=0证起.新知探究0n0n(2)第二步——归纳递推新知探究“假设n=k(kN*，k≥n0)时命题成立，证明当n=k+1时命题也成立”,其本质是证明一个递推关系，归纳递推的作用是从前往后传递，有了这种向后传递的关系，就能从一个起点（例如n=1）不断发展，以至无穷.如果没有它，即使前面验证了命题对许多正整数n都成立，也不能保证命题对后面的所有正整数都成立.注意用数学归纳法证明命题时，难点和关键都在第二步，而第二步主要在于合理运用归纳假设，即以“n=k时命题成立”为条件，结合其他数学知识，证明“当n=k+1时命题成立”.不能不使用“n=k时命题成立”这个条件，而直接将n=k+1代入命题，便断言此时命题成立因为这样的“证明”并不推出递推关系：n=k时命题成立n=k+1时命题也成立.新知探究归纳数学归纳法的适用范围：数学归纳法一般被用于证明某些与正整数n(n取无限多个值)有关的数学命题，但是，并不能简单地说所有与正整数n(n取无限多个值)有关的数学命题都可以用数学归纳法证明，一般说，从n=k时的情形过渡到n=k+1时的情形，如果问题中存在可利用的递推关系，则数学归纳法有用武之地，否则使用数学归纳法就有困难.新知探究用数学归纳法证明　提示∈222*n(n+1)(2n+1)1+2++n=(nN).6…2(1)n=111+121+1\"1=\".6在第一步奠基中，验证时命题成立，即证明命题（）（）新知探究∈222*n(n+1)(2n+1)1+2++n=(nN).6…2(1)n=111+121+1\"1=\".6在第一步奠基中，验证时命题成立，即证明命题（）（）2222222(2)“1+2++kk(k+1(2k+1)=,61+2++k+(k+1)(k+1)[(k+1)+1][2(k+1)+1]=6在第二步归纳递推中，就是要证明条件命题假设）那么”.证明的关键是，如何从n=k时的情形过渡到n=k+1时的情形，即：要证明n=k+1时等式成立，应如何利用n=k时等式成立这个假设.新知探究2222222(2)“1+2++kk(k+1(2k+1)=,61+2++k+(k+1)(k+1)[(k+1)+1][2(k+1)+1]=6在第二步归纳递推中，就是要证明条件命题假设）那么”.当时，左边，右边，等式成立，即，那么，假设当∈时等式成明：立证*2222222222=1=11(1+1)(21+1)==16.k(k(1)+1)(2k+1)1+2++k=6k(k+1)(2k+1)=+(k+1)6n=1(2)n=k(kN)1+2+k(k++k1)(2k+1)+6(k+1+(k+))=16新知探究即当时等式也成，立2(k+1)[(k+1)+1][(k+1)(2k+7k+6)=6(k+1)(k+2)(2k+3)2(k+1)+1]6n=k+1=6=.根据（1）和（2）,可知等式对任何正整数都成立.这句是不可缺少的！当时，左边，右边，等式成立，即，那么，假设当∈时等式成明：立证*2222222222=1=11(1+1)(21+1)==16.k(k(1)+1)(2k+1)1+2++k=6k(k+1)(2k+1)=+(k+1)6n=1(2)n=k(kN)1+2+k(k++k1)(2k+1)+6(k+1+(k+))=16即当时等式也成，立2(k+1)[(k+1)+1][(k+1)(2k+7k+6)=6(k+1)(k+2)(2k+3)2(k+1)+1]6n=k+1=6=.分析1234n11111447710(3n-2)(3n+1)SSSSS.已知数列，，，，，，计算，，，，根据计算结果，猜想的表达式，并用数学归纳法进行证明新知探究（1）猜想的表达是的关键是猜想其分母的表达式.观察的分母可以发现，第一项为4后面的每一项比前一项增加3，于是，我们猜想：的分母是首项为4，公差为3的等差数列.写出这个等差数列的通项公式后，就容易猜想出的表达式.1234SSSS，，，nSnSnS(2)用数学归纳法证明时，要注意从n=k时的情形到n=k+1时的情形是怎样过渡的，即要证明n=k+1时等式成立，应如何利用n=k时等式成立这个假设.1234n11111447710(3n-2)(3n+1)SSSSS.已知数列，，，，，，计算，，，，根据计算结果，猜想的表达式，并用数学归纳法进行证明1234SSSS，，，nSnSnS解：123411S==;144112S=+=;4477213S=+=;771010314S=+=.10101313可以看到，上面表示四个结果的分数中，分子与项数n一致，分母可用项数n表示为3n+1,于是可以猜想nnS=3n+1新知探究123411S==;144112S=+=;4477213S=+=;771010314S=+=.10101313nnS=3n+1当时假设当∈时猜想，左边，右边，，，成即立1*n=1n=k(kN1(1)=S=4n11===3n+131+14(2)111++++14477101k=(3k-2)(3k+1)k1)3+下面我们用数学归纳法证明这个猜想.新知探究当时猜想也成立那么，所以，2111++++144771011+(3k-2)(3k+1)[3(k+1)-2][3(k+1)+1]k13k+4k+1=+=3k+1(3k+1)(3k+4)(3k+1)(3k+4)(3k+1)(k+1)k+1==(3k+1)(3k+4n=k+)3(k+1)+11.根据(1)和(2),可知等式对任何正整数都成立.当时假设当∈时猜想，左边，右边，，，成即立1*n=1n=k(kN1(1)=S=4n11===3n+131+14(2)111++++14477101k=(3k-2)(3k+1)k1)3+当时猜想也成立那么，所以，2111++++144771011+(3k-2)(3k+1)[3(k+1)-2][3(k+1)+1]k13k+4k+1=+=3k+1(3k+1)(3k+4)(3k+1)(3k+4)(3k+1)(k+1)k+1==(3k+1)(3k+4n=k+)3(k+1)+11.nmm11--1时，(1+x)m≥1+mx；（Ⅱ）对于n≥6，已知n111--11+x>0，，于是在不等式k(1+x)1+kx≥两边同时乘以1+x得k2(1+x)(1+x)(1+kx)(1+x)=1+(k+1)x+kx1+(k+1)x≥≥所以k+1(1+x)1+(k+1)x.≥即m=k+1时，不等式也成立.综合（ⅰ）（ⅱ）知，对一切正整数m，不等式都成立．课堂练习2x>-11+x>0，，k(1+x)1+kx≥k2(1+x)(1+x)(1+kx)(1+x)=1+(k+1)x+kx1+(k+1)x≥≥k+1(1+x)1+(k+1)x.≥（Ⅱ）证：当n≥6，m≤n时，由（Ⅰ）得m1m1+1->0n+3n+3，≥于是nnmm11-1-=n+3n+3≤mnm111-0n+3n+3，≥nnmm11-1-=n+3n+3≤mnm111-